Future climate-driven escalation of Southeastern Siberia wildfires revealed by deep learning

Fire-related datasets

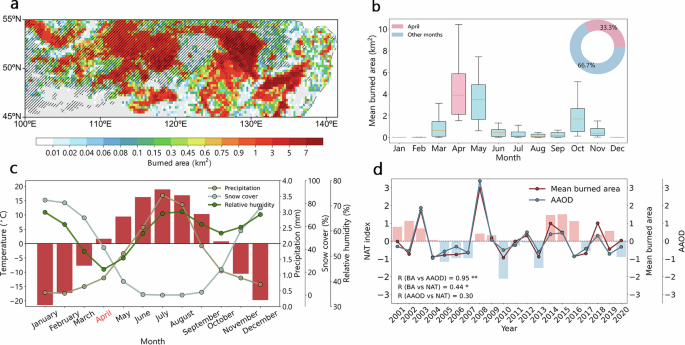
We used a global gridded monthly BA product for the period 2001–2020 from the FireCCI version 5.138 with a spatial resolution of 0.25° × 0.25° to reveal the variability of the SES wildfires. This product is generated by the global BA mapping algorithm based on spectral information from the MODIS (Moderate Resolution Imaging Spectroradiometer) sensor developed by the European Space Agency’s (ESA) FireCCI team. We also included two additional monthly BA products for intercomparison and to verify the relationship between BA variability and the NAT mode, including the Global Fire Emissions Database Version 4 (GFED4, 1996–2016)39 and MODIS MCD64 (MCD64CMQ, 2001–2020)40, both with a spatial resolution of 0.25° × 0.25°. Here, the FireCCI product was chosen as the most appropriate product because it is more sensitive than other global BA products in detecting small burned patches15. However, instead of using the FireCCI dataset as the training set when developing the BA prediction model, we made use of the FireCCILT11 global gridded BA product due to its longer available time span (1982–2018) and comparable performance. The FireCCILT11 dataset (0.25° × 0.25° resolution) was assembled using the long-term data record from the Advanced Very High-Resolution Radiometer imagery, and it has been previously applied to reveal the relationship between global climate teleconnections and BA changes15. The regionally averaged BA time series in April in SES for the above four products exhibited high consistency over the overlap period (2001–2016), with the correlation coefficient (R) varying from 0.54 to 0.91 among the products.

Wildfires exert a substantial environmental impact through the emission of copious smoke aerosols—predominantly black carbon and organic carbon. These aerosols possess a high capacity for solar radiation absorption and are known to have detrimental effects on human health. Moreover, they disrupt the radiation balance within the Earth–atmosphere system, thereby influencing weather patterns and climate. To examine the correlation between the BA and smoke aerosols, the AAOD data from the MERRA-2 reanalysis41, with a resolution of 0.5° × 0.625°, were used. Specifically, AAOD is calculated by subtracting the total scattering of aerosols from their total extinction.

Climate data

We analyzed atmospheric fields with a horizontal resolution of 0.5° × 0.5°, including surface temperature, relative humidity, soil moisture, and snow depth from the European Centre for Medium-Range Weather Forecasts Reanalysis version 5 Land (ERA5-land) reanalysis dataset (2001–2020)42. In addition, we used the geopotential height and winds at 500 hPa from the ERA5. The North Atlantic Tripole (NAT) index is calculated based on the difference in SST anomalies in three regions: A1 − A2 + A3; where A1 is bounded by 32° − 38°N and 70° − 60°W, A2 is bounded by 50° − 55°N and 30° − 25°W, and A3 is bounded by 15° − 20°N and 45° − 35°W43. The SST data, at a spatial resolution of 1° × 1°, are obtained from the Met Office Hadley Centre and have undergone detrending prior to calculation44. This NAT index is indicative of the variability in the atmospheric circulation over Eurasia.

We used the permafrost extent datasets produced by ESA for the Northern Hemisphere for the period 2003–2019 to characterize regional soil properties45. PET and PPT data from the Climatic Research Unit (CRU) were also used, primarily to measure the degree of local drought46. The drought index (i.e., P/PET) was derived by dividing PET by PPT.

Wave ray

In this study, we used horizontal and meridional winds at 200 hPa from ERA5 for April 2000–2020 to calculate the propagation pathways of atmospheric disturbance–induced wave trains in the upper troposphere over the North Atlantic. For this purpose, we adopted the concept of wave rays, viewed as trajectories along which wave energy transmits at the group velocity. The orientation of a wave ray is defined by the direction of the group velocity’s tangent at a given location. The mapping of this tangent onto the longitude (X) and latitude (Y) axes can be calculated using the relevant equations:

where \({{\rm{c}}}_{{\rm{g}}}=({{\rm{c}}}_{{\rm{gx}}},{{\rm{c}}}_{{\rm{gy}}})\) denotes the group velocity. In the framework of wave theory linearized over the zonal mean flow, as described by Hoskins and Karoly (1981), the group velocity is expressed as:

where (k) and (l) are the zonal and meridional wave numbers, respectively, and (\({\bar{{\rm{q}}}}_{{\rm{y}}}\)) represents the meridional gradient of the basic-state absolute vorticity. For stationary waves, the dispersion relation links the wavenumbers with the basic-state properties, which is expressed as:

where (\({\bar{{\rm{u}}}}_{{\rm{M}}}\) = \({\rm{U}}/\cos {\rm{\varphi }}\)) represents the zonal mean zonal wind in the Mercator Projection. These formulas have been utilized in the analysis of a longitudinally varying flow to examine the influence of zonal flow variations on wave propagation, as explored in previous studies47,48.

In this study, we use local values of the basic state, rather than zonal mean quantities, in our wave-ray calculations. The basic state is defined as the smoothed 200-hPa composite-mean zonal wind, exceeding one standard deviation. Meridional wavenumber values are computed by solving Eq. (3) for the given flow and zonal wavenumbers of 1–5. To generate wave rays stemming from the region (0°N–60°N and 300°E–360°E), we integrate Eq. (2). The integration period is 30 days with an hourly time interval.

Sensitivity experiments

To elucidate the influence of the NAT mode variability on SES wildfires in April, we conducted two experiments on the sensitivity of atmospheric circulation simulations to SST forcing using the Community Atmosphere Model version 5 (CAM5), an integral component of the Community Earth System Model version 1.2.2 (CESM1.2.2), a comprehensive coupled climate system model49. CAM5 incorporates a finite-volume dynamical core with 32 vertical tiers stretching from the surface to ~3-hPa50. The simulations were carried out at a resolution of 1.9° × 2.5° (latitude × longitude).

The integration of the control experiment lasted 43 years, with the first three years reserved for spin-up. The model integrates the interactive atmosphere (CAM5) with data-driven ocean, sea-ice, and land components, incorporating closed quasi-biennial oscillation forcing. All external forcings, both anthropogenic and natural, are derived from CESM’s native input data (https://svn-ccsm-inputdata.cgd.ucar.edu/trunk/inputdata/). For the sensitivity experiments, we defined the SST experimental field for the extreme positive (negative) phase of the NAT mode by adjusting the model’s default SST field with the addition (subtraction) of the mean field for those years in which the NAT index is greater (less) than 1.5 (−1.5) times the standard deviation for the baseline period of 1950–2000. The difference between the outputs of the control and sensitivity simulations can be regarded as the response of the atmospheric circulation, along with the anomalies in the local meteorological drivers that instigate wildfires, to the phase transitions of the NAT mode.

CMIP6 outputs

Historical and future simulations of seven meteorological variables, including surface temperature, PPT, PET, surface relative humidity, snow depth, soil moisture, and SST data, with the first ensemble member (“r1i1p1f1”) within Phase 6 of the Coupled Model Intercomparison Project (CMIP6)51 were used. CMIP6-based historical (1982–2014) simulation data were utilized to establish a data-driven prediction model, while future (2015–2100) projected data under two contrasting emission scenarios, a moderate-emission scenario (SSP2 − 4.5) and a higher-emission scenario (SSP5 − 8.5), were employed to assess future climate conditions and predict the potential severity of wildfires in SES.

The skill of various climate models in simulating atmospheric variables varies significantly. To address this, we implemented a robust physical process–based selection procedure to evaluate the performance of each CMIP6 model in simulating relevant variables and to exclude those models that failed to meet predefined threshold conditions at each step of the assessment. Our model selection protocol encompassed five steps: (1) a correlation analysis was conducted between the historical (1970–2014) NAT index in April calculated from Hadley SST data and that from CMIP6-based SST data, and models with R R R > 0; (4) a correlation analysis was further performed between the surface temperature and snow depth to exclude models with R > 0 from the remaining models in the first three steps; and (5) after performing the above four steps, models with all seven variable outputs available simultaneously were identified in the remaining models.

This rigorous selection method ensured that the final CMIP6 model chosen was adept at reproducing the mechanisms by which NAT-driven changes impact local meteorological factors that regulate wildfires in SES. Upon completing the first three steps outlined above, only three CMIP6 models remained: ACCESS-CM2, CESM2-WACCM, and FIO-ESM-2-0. Ultimately, after all criteria were applied, only the CESM2-WACCM model52 from the National Center for Atmospheric Research met the requirements. Notably, the lower atmosphere simulations in the CESM2-WACCM model are based on the CAM model, consistent with those used in the sensitivity experiments. Consequently, output from the CESM2-WACCM was used for analyzing the projected changes in future SES wildfires in April.

Deep learning for BA projections

Climate-driven BA prediction remains challenging due to the spatiotemporally heterogenous responses of BAs to climate variability. In recent years, advances in machine learning approaches, especially deep learning (DL), have provided a valuable toolkit for uncovering the complex relationships between regional wildfires and climate change. DL has been widely used to identify the key drivers of wildfire variability and to develop forecasting systems for wildfire activity at global and regional scales53,54.

Here, we developed a BA prediction model leveraging on a long short-term memory (LSTM) framework55 to establish a robust nonlinear relationship between the historically observed BA variability and key climate drivers. The LSTM model, a variant of a recurrent neural network (RNN), has advantages in capturing both short- and long-term dependencies in long time sequences, such as the SES wildfires series modulated by changes in climatic conditions. Compared with a traditional RNN, an LSTM filters out useless information from the time series while retaining useful information by introducing a gating mechanism55. Although LSTM can be employed for spatiotemporal sequence prediction, it does not take spatial features into consideration. Here, we extend the LSTM framework to have the convolutional structure in both the input-to-state and state-to-state transitions, and we propose the convolutional LSTM (ConvLSTM) model56 to build a trainable model for reasonably projecting future changes in SES wildfires. The ConvLSTM-based wildfire prediction model was trained using seven meteorological predictors (surface temperature, PPT, PET, P/PET, surface relative humidity, snow depth, and soil moisture) derived from the CESM2-WACCM historical output in CMIP6 and the longest available BA records from FireCCILT11 spanning 1982 to 2012; the remaining two years (2013 and 2014) were used for model evaluation. The trained wildfire prediction model was then utilized to project future changes in the BA in SES by using future projected data from the CESM2-WACCM simulation for the SSP2-4.5 and SSP5-8.5 pathways in CMIP6, covering the period from 2015 to 2100.

The satellite-retrieved BA data exhibit high spatial variability, resulting in significant differences in values between neighboring grids. To address this issue, we used a two-dimensional convolution kernel in PyTorch57 to aggregate the 4 × 4 grids into one grid, creating a final resolution of 1.0° × 1.0°. The meteorological fields from CESM2-WACCM, with a spatial resolution of 1.25° × 0.9°, were also adjusted to the same grid resolution through nearest-neighbor interpolation. Before running the ConvLSTM model, we packaged the data in batches as well as in time series. Here, the ConvLSTM model is designed for fitting purposes, that is, the length of the time series of the input data is the same as the length of the output time series. The following is a detailed description of the model structure. Specifically, our BA prediction model consists of three main parts: a ConvLSTM layer, a convolutional layer, and a fully connected (FC) layer (Fig. 3). For each batch, when the meteorological fields with seven features are input into the model, the hidden layer in the ConvLSTM layer first extracts the features up to 16. Subsequently, the convolutional layer further scales the features to 256 and filters out the redundant features through adaptive pooling (AP). Finally, the time series of BA spatial fields are output by an FC layer. In this study, we extracted the BA data in April from the full model-predicted BA time series for the period 2015 to 2100 and used it for analysis.

Statistical analysis

We used correlation analysis to ascertain the relationships among wildfire activity, NAT mode, atmospheric circulation patterns, and local meteorological drivers. Furthermore, we examined the projected changes in future meteorological conditions as simulated by CMIP6 through linear trend analyses. The statistical significance of the correlation analyses, trend estimations, and composite differences was determined using a two-sided Student’s t-test.